Calculation of linked flux
The linked flux is defined as the path integral of the magnetic vector potential:
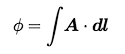
where the path is along the current flow in the conductor. For bulky conductors, the above path integral can be approximated by a volume integral. This definition of linked flux works even for open conductors. The linked flux depends on the currents flowing in all the conductors.
Calculation of mutual inductance

M points
To compute the mutual inductance between two objects, set the current equal to zero in all but one of the objects, set the current in that object equal to one ampere, and measure the linked flux in the other object. The linked flux (in units of weber, or Wb) in this situation is numerically equal to the mutual inductance (in units of Henry, or H).
The linked flux is calculated at what we call the M points. Assuming nothing about the symmetry of the magnetic field in which the conductor finds itself, the M points must sample the entire volume of a bulky conductor. For a solenoid the M points are distributed as shown, with the number of azimuthal steps determined by the user. In the azimuthal planes the spacing of the points is equal to resolution specified for the conductor.
Calculation of self-inductance

L points
The self-inductance of a conductor is numerically equal to the linked flux when the only source of magnetic field considered is the object itself and when the current through the conductor is one Ampere. For example, if in this situation the linked flux is 0.01 Wb, then the self-inductance is 0.01 H.
For calculation of self-inductance the linked flux is calculated at what we call the L points. For axially symmetric conductors, the vector potential need only be computed at one azimuthal coordinate, which makes the calculation of self-inductance very fast. The density of the points is equal to the resolution specified for the conductor.
Implemented calculations
The following table indicates the inductance calculations that are presently implemented in BiotSavart:
| Conductor | Linked flux | Self-inductance |
|---|---|---|
| Loop | YES | YES |
| Solenoid | YES | YES |
| Revolved | NO | NO |
| Wire | YES | YES |
| Racetrack | NO | NO |
Customers take note: On request we can implement those calculations that are not yet implemented, if needed for your work.

